La conjecture des lits superposés est fausse

En mathématiques, certaines conjectures suscitent des convictions très fortes chez les spécialistes – par exemple, peu de mathématiciens pensent que l’hypothèse de Riemann ou la conjecture de Syracuse sont fausses. Cependant, il arrive parfois qu’une affirmation que tout le monde pensait vraie s’avère fausse. C’est ce qui s’est passé pour la « conjecture des lits superposés », en théorie des graphes : début octobre 2024, Nikita Gladkov et Igor Pak, de l’Université de Californie à Los Angeles, ainsi qu’Aleksandr Zimin, du MIT (le Massachusetts Institute of Technology), tous aux États-Unis, ont mis en ligne une pré-publication dans laquelle ils présentent plusieurs contre-exemples à une déclaration qui, cependant, a été largement acceptée depuis sa première formulation en 1985.

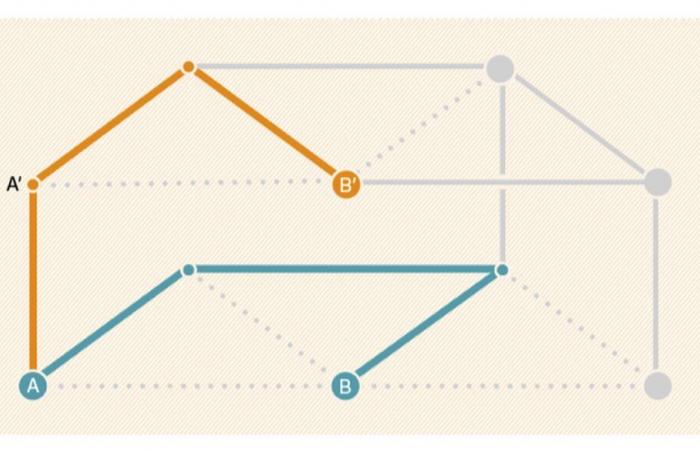
Considérons un graphique G connecté (c’est-à-dire un ensemble de sommets reliés entre eux par des arêtes, formant une structure unique) et dupliquez-le pour obtenir un deuxième graphe G’identique. Choisissons maintenant un sous-ensemble des sommets de Get reliez chacun d’eux par une nouvelle arête au sommet correspondant de G’. De cette manière, nous construisons un nouveau graphe ressemblant à un lit superposé dont la couchette inférieure est le graphe Gcelui en haut du graphique G’et les montants sont ces arêtes joignant les sommets cousins ​​de G et G’. Imaginez maintenant que chaque bord de ce « lit superposé » disparaisse avec une certaine probabilité p. Comme G était connecté (en un seul morceau), il était toujours possible, dans le graphe initial, de joindre deux sommets quelconques de G – disons UN et B – par un chemin continu d’arêtes de G. Comme certains sommets de G étaient connectés aux sommets correspondants de G’et ça G’était également connecté, il était également possible, dans le lit superposé initial, de connecter UN au sommet de G’correspondant à B – appelons-le B’. Mais que se passe-t-il une fois que certains bords sont supprimés de manière aléatoire ? La conjecture de 1985 stipule que, dans le lit superposé final (après suppression probabiliste des bords), la probabilité qu’un chemin joignant UN et B est supérieure à la probabilité qu’un chemin rejoignant UN et B’.

En travaillant sur cette conjecture, Nikita Gladkov et ses collègues se sont inspirés des résultats de Lawrence Hollom, doctorant à l’Université de Cambridge, en Angleterre, qui étudiait également le problème, dans un premier - pour démontrer que l’affirmation était correcte. Comme le résultat lui résistait, il se concentra sur la même question transposée à des objets un peu plus « dociles ». » : les hypergraphes, une généralisation des graphes où les arêtes peuvent relier plus de deux sommets. « Comme je ne faisais pas beaucoup de progrès, j’ai commencé à m’intéresser à des problèmes similaires sur les hypergraphes, mais en plus simples. Cependant, j’ai remarqué que pour que la conjecture des lits superposés soit vraie, il fallait que bien d’autres affirmations plus simples soient également vraies… et qu’il allait finalement être très difficile de garantir que ces affirmations seraient toujours vérifiées, toutes en même -. ! » Résultat : le chercheur change d’avis, et, en juin 2024, il présente dans une prépublication un contre-exemple à la conjecture des lits superposés pour les hypergraphes.

C’est à partir de ces travaux que Nikita Gladkov, Igor Pak et Aleksandr Zimin ont tour à tour réussi à construire un contre-exemple à cette conjecture, cette fois pour les graphes, dans le cas où la probabilité de disparition des arêtes vaut p = 1/2. « Notre contre-exemple est un graphique G à 7 222 sommets, explique Nikita Gladkov. C’est énorme, mais cette taille vient du fait que nous l’avons construit à la main à partir de l’hypergraphe de Lawrence Hollom. On comprend donc très bien pourquoi il ne vérifie pas la conjecture ! » Dans ce contre-exemple géant, il y a bien deux sommets UN et B du graphique G comme la probabilité qu’un chemin rejoignant UN et B dans le lit superposé, après suppression de chaque arête avec une probabilité 1/2, est inférieure à la probabilité qu’un chemin joignant UN et B’. Ridiculement plus petit, c’est vrai : la différence de probabilité est inférieure à 10^-4331. Mais plus petit tout de même.

A noter que, toujours dans le cas où p = 1/2, les chercheurs ont identifié un contre-exemple beaucoup plus petit : un graphique G à 82 sommets. Mais cette dernière est moins bien comprise : « On ne sait pas se passer d’un ordinateur pour prouver qu’il s’agit bien d’un contre-exemple », déplore Nikita Gladkov.

Igor Pak aime dire que sur une semaine de recherche en mathématiques, il est bon de consacrer six jours aux preuves et un jour aux contre-exemples. Nikita Gladkov est d’accord : « Peut-être que cet épisode montre que nous devons être plus sceptiques à l’égard des conjectures classiques. Lorsque l’on manipule de grandes structures peu rigides, il existe de nombreux degrés de liberté : cela laisse place à des événements inattendus et contre-intuitifs. »